Pourrais-tu expliquer comment tu arrives aux valeurs " 50% pour 80 et 99% pour 40."
Je ne dis (évidemment) pas que v/2 ne se situe pas entre 0 et v. Par « symétrie temporelle » j’entends c constant, et rien d’autre. Ceci dit je veux bien utiliser la notion de « centre de symétrie ». Mais dans ce cas je dis que le centre de symétrie devrait être v plutôt que v/2. Mon argument en faveur de v plutôt que v/2 est que l’espérance de vie est une moyenne calculée sur base des taux de mortalité par âge.
Désolé, je ne suis vraiment pas très bon en math.
Je ne comprend pas comment v=80 étant symboliquement l’extrémité « fin » du bâton par opposition à l’extrèmité « début » du bâton peut être considéré comme centre de symétrie. Je conçois une symétrie perpendiculaire, voir longitudinale, un point de symétrie équilibrant sa masse attirée par une force de gravité. Mais une symétrie « d’extrèmité » je ne vois pas.
Merci de m’éclairer avec des concepts simples qui me soient accessibles.
Est-il pertinent de considérer la moyenne de l’age de décès comme base de symétrie ou de considérer la valeur médiane de la durée totale de vie ? Ce que nous cherchons avec ev/2 n’est pas une moyenne mais un temps médian à ne pas confondre avec la recherche de la moyenne de la masse monétaire atteinte au temps médian de ev.
Nous parlons bien de temps moyen (ou point médian) d’espérance de vie « ev », pas de la moyenne de l’age de la probabilité de mort.
Je pense que l’introduction de la notion de centre de symétrie dans la TRM vient du fait qu’on utilise « symétrie » pour dire « égalité de traitement » et qu’on se laisse ainsi entraîner dans des considérations géométriques qui ne sont pas ici d’application. Dès lors que c est constant, et quelle qu’en soit la valeur, je ne vois pas en quoi l’égalité de traitement entre générations est fonction de la valeur de la constante. D’où mon choix de simplicité pour v plutôt que v/2. Mais si tu veux absolument interpréter géométriquement ces considérations alors tu peux voir mon « centre de symétrie » non pas entre 0 et 80 mais entre une période de 80 qui finit et une autre qui commence.
Alors ici tu vis un point aveugle. Si tu ne vois pas l’asymétrie résultante d’un c = 0,00001% par exemple, c’est que tu n’as pas compris le sujet du tout.
C’est sans aucun doute possible ce point que tu dois éclaircir.
Pour commencer pourrais-tu réaliser 3 graphes juxtaposés sur 120 ans (comprenant donc la descente après la mort, cf TRM appendice mathématique Relatif), pour 3 valeurs de c :
1°) c = 1% / an
2°) c = 10% / an
3°) c = 50% / an
Sur la même échelle relative en hauteur = la moyenne exprimée en DU soit : 1/c DU dans chaque cas. Une droite marquant cette moyenne dans les 3 cas.
Les graphes juxtaposés étant réalisés que vois-tu, qu’interprètes-tu ?
Quel intérêt y a t’il à une symétrie « simple mathématiquement » s’il en résulte que les générations qui partent décident du monde dans lequel vivront celles qui arrivent ?
Cette monnaie se veut servir à l’économie des vivants, pas à celle des morts.
Pour N constant, il n’y a là aucun « avantage » ni « désavantage », puisque les nouveaux deviennent des anciens. La courbe de R, certes asymptotique, est cependant identique pour tous.
Il ne s’agit pas de la forme, j’insiste sur le fait que sans réaliser les 3 graphes sus-cites la comprehension ne peut se réaliser. Il subsiste un point aveugle dans ta compréhension.
Change les valeurs de la cellule B2, et montre où, pourquoi et comment il y aurait des asymétries entre générations dès lors que c et N sont constants :
Q-R.ods (68,3 Ko)
Je n’ai trouvé à ce jour aucune démonstration de l’affirmation « un c petit avantage les plus âgés, tandis qu’un c grand avantage les plus jeunes ». Ni dans la TRM, ni dans les modules. Il n’y a que des reformulations de la même affirmation.
« Je n’ai trouvé à ce jour aucune démonstration de l’affirmation “un c petit avantage les plus âgés, tandis qu’un c grand avantage les plus jeunes”. Ni dans la TRM, ni dans les modules. Il n’y a que des reformulations de la même affirmation. »
Si tu publiais les 3 graphiques juxtaposés ici même tu répondrais à la première étape de la nécessaire reflexion qui aboutit à une conclusion.
L’argument de l’éventuelle absence de preuve est doublement erroné pour 2 raisons :
-
Bien que la preuve de Perelman ait été publiée, qui peut affirmer qu’il a bien compris qu’il y avait là la preuve ?
-
Quand Poincaré annonce sa conjecture en 1905, est-ce que parce que la preuve de Perelman arrive en 2006 la conjecture était fausse entre 1905 et 2006 ?
Comment Poincaré a-t-il pu annoncer le vrai sans preuve ?
En science véridique l’absence de preuve ne signifie en rien la preuve de l’absence.
Aussi l’homme honnête écoute et réfléchit il ne reste pas à gémir et se plaindre de ce qu’il ne voit pas.
Rien du tout. Avec N et c constants ces exercices ne révèlent aucune asymétrie intergénérationnelle. Il ne pourrait en être autrement puisque la courbe de Rt vaut pour toutes les générations. Ton raisonnement repose sur une définition biaisée que tu as exprimées ailleurs dans ce fil : « On qualifie d’avantage pour les plus anciens le fait que la convergence pour les nouveaux soit lente, et inversement rapide comme avantage pour les nouveaux ». Or il n’y a aucun avantage ou désavantage dans le fait que la convergence pour les nouveaux soit lente, et rapide pour les nouveaux, puisque la courbe certes asymptotique de Rt vaut pour toutes les générations.
PS1 : Ces considérations ne doivent pas être confondues avec le cas d’une variation de c, ce qui induit évidemment une asymétrie temporelle.
PS2 : tu n’as toujours pas répondu à la question posée dans Pourquoi ev/2 ? - #8 par Galuel : Comment arrives-tu à ces chiffres « 50% pou 80 et 99% pour 40 » ?
Mais certainement pas pour tous les humains de ces générations. Tu devrais réellement tracer ces courbes.
Les voici (à nouveau) : R.ods (61,4 Ko)
Tu changes la valeur de c en changeant la valeur de la cellule A2. Les valeurs de R sont dans la colonne D.
Alors bien sûr que, plus la valeur de c diminue, moins la courbe R est incurvée. Mais pour N et c constants, et quelle que que soit leur niveau, cette courbe est la même pour ceux qui sont morts, pour les jeunes et les vieux d’aujourd’hui, et pour ceux qui naîtront demain. Certes, à un instant t les jeunes vivants ne sont pas au même endroit de la courbe que les vieux vivants, mais chacun durant sa vie va passer par les mêmes points. Enfin, bien sûr il y a des gens qui meurent avant ou après 80 ans, et c’est pourquoi l’espérance de vie est calculée sur base des taux de mortalité par âge.
Ainsi pourrais-tu démontrer que « Un c petit avantage les plus âgés, tandis qu’un c grand avantage les plus jeunes » ?
→ Un c petit avantage les plus âgés, tandis qu’un c grand avantage les plus jeunes - #2 par Galuel
Bien sûr que je le pourrais, mais tu tentes d’inverser la charge de la preuve. Des indications pour le comprendre toi-même, mieux le démontrer ou l’infirmer, t’ont été données. Si la démonstration t’était donnée, alors la maîtrise resterait de notre côté et pas du tiens, ce qui n’aurait aucun intérêt.
Et donc libre à toi de ne pas réaliser ni exposer tes résultats. Tu peux pourtant le faire sous la forme d’un graphe que tu peux directement copier/coller sur ce forum, c’est très simple.
Très simple oui en effet.
Toujours pas les 3 graphes demandés sur 160 ans, avec v = 80, et visualisation de la moyenne dans les 3 cas.
Si on regarde un objet sur une face, on ne voit pas la 3D, encore moins l’intérieur, et on ne parle même pas de sa création, son évolution et sa fin.
Nul n’est plus aveugle que celui qui ne veut pas essayer de comprendre.
g/v = 9 mois / 80 ans = (9/12 ans) / 80 ans = 0,0094 = 0.94% et non 9,94% et encore moins 9,94%/an, ou alors j’ai loupé quelque chose.
Favoriser les nouveaux, ou favoriser les anciens ? Cette phrase peut avoir plusieurs sens.
Si on appelle « anciens » ceux qui ont vécu leurs vies dans l’ancien temps et « nouveaux » ceux qui ont vécu après eux, ils auront tous créé la même quantité relative de monnaie, selon le principe de base de la TRM. Aucun ne sera favorisé.
On peut, de façon différente, appeler « ancien » un membre créant de la monnaie depuis longtemps et « nouveau » un membre récemment entré dans la monnaie. Dans cette acception, le terme « favoriser » peut encore avoir plusieurs sens.
Les anciens auront toujours créé plus de monnaies que les plus jeunes, tout simplement parce qu’ils auront eu plus de temps pour cela. En ce sens, toute monnaie libre favorise les anciens.
En quelle proportion les anciens sont-ils favorisés par rapport aux nouveaux ? Si on choisit pour unité la masse monétaire moyenne par créateur en régime stationnaire, la masse monétaire créée par un membre au cours de sa vie, à l’instant t après son entrée dans la monnaie, vaut :
m(t) = 1 / c (1 - e^(-c t))
Comparons la masse monétaire créée par un nouveau, par exemple au milieu de sa vie (t = v / 2) à celle créée par un ancien à la fin de sa vie (t = v) et calculons le rapport r des deux :
r = m(v / 2) / m(v) = (1 - e^(-c v / 2)) / (1 - e^(-c v))
Pour une durée de vie v = 80 ans, calculons r en fonction du taux de croissance c de la monnaie. On obtient la courbe suivante :
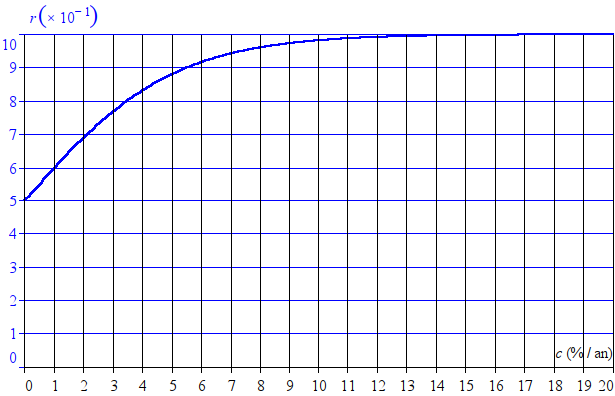
Conclusion : plus c est élevé, moins les anciens sont favorisés par rapport aux nouveaux parce que la masse monétaire moyenne est atteinte plus vite. On peut aussi dire, que, par rapport à une valeur plus faible, un valeur élevée de c favorise les nouveaux.
« Aucun n’est favorisé » ; « les anciens sont favorisés par rapport aux nouveaux » ; « plus c est élevé, plus les nouveaux sont favorisés par rapport aux anciens » : faites votre choix.