Une monnaie symétrique dans une économie avec des biens de valeur stable

tschoatsch · Juin 27, 2020, 3:38

Bonjour tout le monde,

ça fait un moment que je connais la TRM, et elle ne cesse de me fasciner. Pourtant, je me pose des questions sur l’interaction d’une monnaie symétrique avec des objets de valeur stable. L’impression que j’ai c’est que dès qu’il y a des biens de valeur relativement stable à acheter en monnaie symétrique, chaque utilisateur qui veut augmenter sa richesse a raison de les acheter au plus vite. Ou autrement dit, chaque utilisateur qui veut augmenter sa richesse a raison de se débarrasser le plus rapidement possible de la plus grande quantité de monnaie symétrique possible. Si c’est vrai, ça voudrait dire que des homo oeconomici qui choisissent d’utiliser une monnaie symétrique pourraient s’enrichir au détriment des autres utilisateurs. Ou que personne veut plus vendre des biens de valeur stable dans la monnaie.

J’ai construit un modèle simple (inspiré du module Galilée) pour clarifier comment j’arrive à mon impression. Le modèle se trouve en PJ, une petite description suit:

MODÈLE

Le modèle simule une économie avec trois individus (A, B et C) et 30 biens identiques et non-périssables. Il n’y a pas de production de biens.

Dans l’année zéro, A, B et C ont 10 biens chacun. Ils/Elles se décident d’adopter une monnaie symétrique pour faciliter leurs échanges. Ils/Elles se donnent chacun/e 100 entités de monnaie. Chaque année, ils/elles vont recevoir un DU correspondant à 10% de la masse monétaire moyenne de l’année précédente. S’il n’y aura pas d’échanges, chacun/e aura donc toujours un total correspondant à 10 DU, bien que la masse monétaire augmente de façon exponentielle.

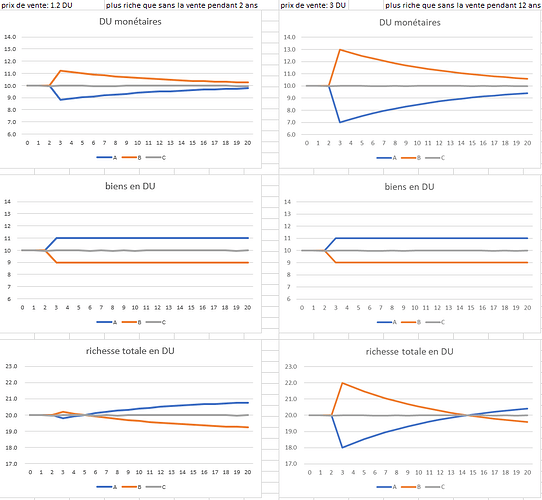
Les deux premières années, il n’y a pas d’échanges. En année 3, A voudrait acheter 8 biens. Vu qu’il n’y a que les 30 biens dans l’économie, A propose de payer un trentième de la masse monétaire par bien, ce qui correspond à un prix de 1 DU. B lui vend 2 biens, et C lui en vend 6.
A donne donc 2 DU à B, et 6 DU à C. Après, il n’y a plus d’échanges.

Voici le développement de leurs DU au fil de 20 ans:

DU1

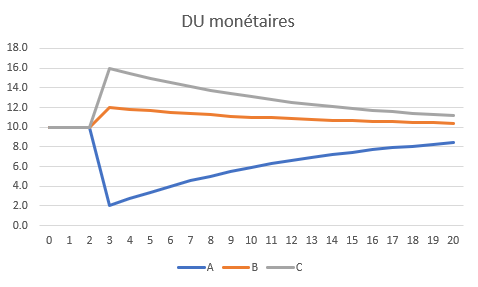
Au début, A, B et C ont 10 DU chacun. En année 3, A tombe à 2 DU et les autres en auront plus. Au fil des années, les différences s’atténuent, et les trois se rapprochent de la moyenne (de 10 DU).

Voici le développement de leurs biens, évalués en termes de DU:

DU2

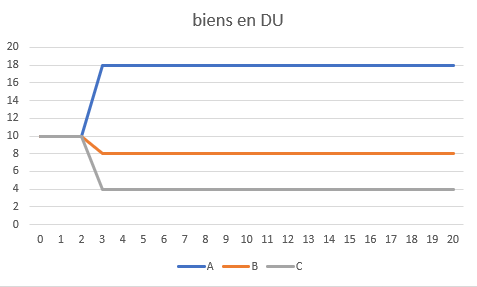
Au début, ils/elles ont des biens valant 10 DU chacun. À partir de l’année 3, A a des biens valant 18 DU, B a des biens valant 8 DU et C a des biens valant 4 DU. Cela ne change pas au fil des ans.

Voici le développement de leur richesse totale (la somme des DU monétaires et des biens évalués en termes de DU):

DU3

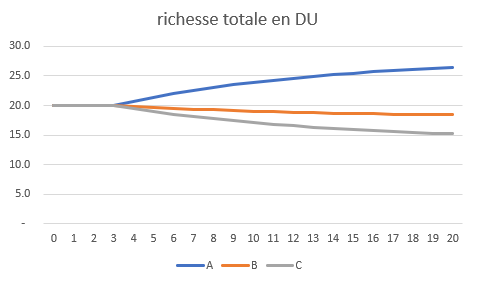
À partir de l’année 3, celle de A croît, et celles de B et C diminuent. Il n’y a pas de convergence au fil des ans, seulement une stabilisation des différences.

INTERPRÉTATION

À moi, il me semble que chaque homo oeconomicus dans un système symétrique va raisonner comme A: J’achète le maximum de biens de valeurs stable que je peux, et après, vu que je suis pauvre d’argent, la monnaie symétrique me lèvera automatiquement à la moyenne monétaire. Ainsi, dès le début, je suis riche en biens, et après quelques années, je serai en plus aussi riche que les autres en termes de monnaie.

QUESTIONS

*) Est-ce le résultat attendu?

*) Est-ce qu’il y a des alternatives pour déterminer les prix ou d’autres interventions (taxation des biens peut-être, si possible) qui évitent les conséquences inéquitables montrées?

*) Est-ce qu’une monnaie symétrique est simplement pas conçue pour une économie avec des biens de valeur stable ou des acteurs qui veulent accroître leur richesse / homo oeconomici?

*) Qu’est-ce qui fait que ces résultats ne se retrouvent pas dans la réalité de la June (j’assume)?

*) Est-ce qu’il y a des problèmes méthodologiques ou dans les hypothèses du modèle?

Tout autre retour sur les thèmes évoqués est aussi apprécié, bien sûr

D’ailleurs, @yyy et @jytou, j’ai lu votre discussion sur la simulation avec des IA, est-ce qu’il y a des nouvelles là-dessus depuis janvier 2019? Le résultat obtenu ici me semble une hypothèse qu’on pourrait formidablement tester avec un tel modèle, et trouver des solutions peut-être.

Merci d’avoir lu jusqu’ici, j’ai essayé de faire plus court, mais pas réussi

trm.zip (26,6 Ko)

Galuel · Juin 27, 2020, 3:51

1°) Démontre en quoi une monnaie asymétrique produirait un résultat différent ?

2°) Puisque tous les acteurs peuvent être au courant de la stratégie à suivre, comment donc pourrait-il y avoir des perdants ?

3°) L’hypothèse

Est un cas d’hypothèse spécifique (théorique), dont l’existence est réfutée par la TRM.

yyy · Juin 27, 2020, 4:47

Qu’entends-tu par cela ? Que des objets sont estimés en DU, et que le montant de cette estimation reste la même pour tout le monde, maintenant et plus tard ?

Tout à fait, je parle également de ce phénomène sur ce forum Que j’ai synthétisé ici, avec d’autres phénomènes : Convergence des comptes, intérêt de dépenser/donner, et répartition des parts relatives à l'entrée de nouveaux membres

Pour acheter le maximum de biens, c’est à dire dépenser au maximum ses junes, il faut des vendeurs Si tout le monde achète, qui vend, et pourquoi ?

Je te laisse lire mes conclusions dans le lien

je cherche toujours à réaliser une simulation sans règles ad-hoc Mais ça semble toucher au cœur même de l’économie : comment se forment les prix ?

Je cherche un modèle qui me semble pertinent, mais je n’en trouve pas !

jytou · Juin 27, 2020, 7:07

Un exemple de « bien de valeur stable » ? Je ne vois d’ailleurs pas en quoi cela permettrait d’accroître sa richesse dans la mesure où tout le monde va faire pareil et soit les « biens en question » (si tant est qu’ils existent…) vont voir leur prix augmenter sérieusement pour se stabiliser assez haut rendant donc ce schéma assez peu intéressant, soit les humains vont au contraire s’en désintéresser parce que thésauriser ne sera pas leur principale préoccupation.

Le meilleur moyen d’« accroître ta richesse » dans une économie sous monnaie libre, c’est de produire constamment quelque chose dont les humains ont besoin et qu’ils sont prêts à payer un prix assez élevé pour X ou Y raisons (tu es le seul à en produire, tu es plus doué que les autres et la qualité de tes produits est bien supérieure, tu est renommé, tu as une super équipe marketing, etc.).

Il me semble que le syndrome « je vais tout faire pour m’enrichir à moindre coût » est typique d’une société sous monnaie-dette, mais je ne suis pas sûr que ce soit le comportement typique des humains sous monnaie libre. Ce n’est en tout cas pas ce qu’on observe dans les Ğeconomicus, mais il nous reste à l’expérimenter dans la vraie vie pour voir où on en est.

Je n’ai pas avancé sur les simulations, je suis sur autre chose (à suivre).

Edit : je n’avais pas vu les réponses précédentes, désolé pour les doublons…

jytou · Juin 27, 2020, 7:11

C’est effectivement aussi l’un des sujets les plus ardus pour ce type d’IA. J’y ai aussi pas mal réfléchi. Tout est question d’échelle de valeurs, d’utilité ressentie à un instant t entre tel ou tel objet ou service, chose pour lesquelles les IA risquent de se comporter de manière bien différentes (parce que plus « rationnelles ») des humains. La subjectivité inhérente à l’humain est quelque chose de très difficile à modéliser. Il reste les réseaux de neurones, qui se rapprochent un peu plus des cerveaux humains.

Ça vient, ça vient.

tuxmain · Juin 27, 2020, 8:07

Dites que c’est réfuté si vous voulez, mais on constate que certains trucs (ou ğtrucs pour ceux qui ont réfuté la notion de trucs) sont relativement stables sur le marché. Le prix du nem en DU n’a pas changé pendant des mois.

Ce n’est pas une hypothèse si coûteuse de penser que l’estimation moyenne de certains biens restera très probablement semblable à quelques jours d’intervalle.

Pour la simulation, pourquoi pas. Plutôt qu’une IA on peut commencer par de bêtes caractéristiques de type jeu de rôles, avec des probas. On pourrait même simuler à la fois la monnaie et la TdC, et pourquoi pas plusieurs monnaies dont des UNL…

Galuel · Juin 28, 2020, 7:36

Eh bien dans ce cas puisque tu y crois, tu n’as qu’à suivre ta stratégie gagnante. Nous te prenons donc pour un premier test expérimental, note bien tout.

Hors vérification expérimentale toute prédiction est du pur charlatanisme.

Donc rendez-vous dans 10 ans pour vérifier si tu as réussi.

tschoatsch · Juin 28, 2020, 9:22

Merci beaucoup de vos réponses, elles étaient extrêmement clarifiantes!

Surtout, c’était très élucidant de réfléchir sur quoi j’entendrais par un bien de valeur stable. Je pense que je pensais qu’on aurait un tel bien (par exemple) si l’on avait:
(1) une somme invariable de produits P identiques, non-périssables et non-détériorables (donc identiques entre eux et à travers le temps) et
(2) une masse monétaire stable (soit en DU).
Dans un tel cas, j’aurais dit que « un DU achète toujours la même quantité de produits », et que le prix d’un produit en DU est de M/P. Grâce à vos commentaires, je me rends compte que (assez évidemment en fait) c’est pas le cas, et que le vendeur peut bien demander un prix plus élevé que M/P.

yyy, merci pour le lien, j’avais pas rencontré lors de mes recherches. Tu argumentes que c’est raisonnable de vendre un bien en monnaie symétrique si l’on veut acheter un bien vendu en monnaie symétrique qui coûte plus cher que ce qu’on a. En jouant un peu avec mon modèle, j’ai trouvé une autre façon de réfléchir sur la question quand vendre. C’est de se poser la question « pendant combien de temps veux-je être plus riche que si je vends pas? ». Voici l’illustration avec les graphes d’auparavant.

Ici, A est l’acheteur, B est le vendeur dans le cas où il vend, et C est le vendeur dans le cas où il vend pas. Ce qui nous intéresse c’est uniquement les différences entre B et C. Dans les graphes dans mon dernier post, on voit que, si B vend le bien (pour lequel M/P == 1 DU) à 1 DU, il commence à perdre en richesse immédiatement. Dans la première colonne ici, on voit que s’il vend à 1,2 DU, il sera plus riche que s’il vend pas pendant deux ans. Dans la deuxième colonne, que s’il vend à 3 DU, il sera plus riche que s’il vend pas pendant 12 ans.

En plus, si l’on divague de l’idée qu’on peut vendre que contre une somme fixe d’argent, il y a bien d’autres arrangements possibles. Par exemple, on peut inverser la position d’acheteur et de vendeur (colonne droite ci-suivant) ou carrément émuler une monnaie « stable » avec des contrats adaptés:

Dans la première colonne ici, A paye B 1 DU en année 3, et 10% d’un DU les années suivantes. On voit que B reste aussi riche s’il vend et s’il vend pas (je sais pas d’où les légères différences dans le dernier graphe viennent, mais sans doute on peut trouver un arrangement où les courbes B et C se superposent). Dans la deuxième colonne, A paye B 12,5% d’un DU dès l’année de la vente. On voit que B sera plus pauvre que s’il vend pas pendant 12 ans, mais qu’il gagnera en richesse après. Ce résultat est l’inverse de l’arrangement où B vend à 3 DU.

Qu’est-ce que vous en pensez? Moi je me pose ces questions:

*) Est-ce que vous pratiquez des contrats comme ceux dans le dernier graphe en June?

*) Est-ce qu’il y a un danger de perdre des bienfaits d’une monnaie symétrique si tous les contrats se feraient comme celui qui émule une monnaie « stable »?

Maaltir · Juin 28, 2020, 9:38

Ne ne comprends pas toutes ces pérégrinations.
Selon moi tout ça c’est de la spéculation, c’est parier qu’un produit aura (dans un futur plus ou moins proche) plus de « valeur » que ce qu’il coûte au moment ou je l’achète.

Tout le monde bénéficiant des mêmes informations, le vendeur sera t il enclin à vendre un produit qui pourrais lui rapporter plus?
Tout cela relève du pari, du grand jeu de casino du monde. Quelque soit la monnaie, je ne crois pas qu’on puisse y changer grand chose.

La monnaie libre, permet me semble t il, d’égaliser le jeu, en « offrant » la même mise de départ.

jytou · Juin 28, 2020, 11:58

Une autre manière de faire « fructifier » ses DU est évidemment l’investissement :

à fonds perdus dans des structures communes dont on risque bien d’avoir besoin un jour ou l’autre, écoles, ponts, etc., si la monnaie est perdue pour celui qui a dépensé, l’investissement, lui, ne l’est pas,
dans des structures dont on espère qu’elles vont

→ pour pouvoir espérer en retirer quelques bénéfices et donc sur le long terme ne pas perdre des DU voire en gagner un peu.

D’où l’idée que des banques en Ğ1 auraient très probablement pas mal de boulot.

nessbyz · Juin 28, 2020, 12:37

perso je compte en étapes moyenne càd la première année de co-création = (365~73o) ainsi dessuite avec une pression neutre de la future symétrie, autrement dit la moyenne des comptes annuelle, les fameux 1oD.u^an (=38ooD.u).

celà programme que tout le monde s’ aligne à une dépense/gain maxi de 73o D.u/an afin que les nouveaux , et pour le moment il n’ y a que ça , puissent échanger quotidiennement en respectant volontairment ou pas la moyenne.

les épargnes dégressives restantes interessantes pour le développement, les ‹ ‹ anciens › › s’ alignent aux nouveaux et à leurs flux moyens, ils peuvent cependant réinvestir leur part conséquente de masse monétaire.

au final deux types de co-création relative, celle qui est quotienne et convergera mécaniquement vers la moyenne des nouveaux autour de un ou deux D.u^an (flux moyen des nouveaux entre eux), puis plus tardivement par rapport à aujourd’ hui, la pression neutre à 1oD.u^an.

les étapes sont là encore stables pour un moment voire tout le temps*.

*hors ‹ ‹ contract › › asymétrique.

ps/ce modèle économique est dû au simple fait que réaliser des échange équitables ou ne rien faire revient quasi au même en mL; la moyenne des échanges idem