La méthode de calcul empirique de « c » la plus aboutie ! c = f(v,x) http://www.creationmonetaire.info/2019/08/c-fvx.html #monnaielibre #trm #duniter #Ğ1
Spéciale dédicace @gerard94 & @Salome_Iris
La méthode de calcul empirique de « c » la plus aboutie ! c = f(v,x) http://www.creationmonetaire.info/2019/08/c-fvx.html #monnaielibre #trm #duniter #Ğ1
Spéciale dédicace @gerard94 & @Salome_Iris
Comme quoi, Gérard a bien fait de te tanner avec ça.
La façon de calculer « c » faisait un peu tâche dans la TRM. Je suis entouré de scientifique dans mon boulot, et je trouvais cet aspect difficilement présentable à mes collègues.
Vivement la publication d’une nouvelle version de la TRM.
A noter : le mot « empirique » est utilisé 3 fois dans ce billet (ça va mieux en le disant, j’aurais bien aimé qu’il apparaisse aussi dans la TRM).
C’est très simple et expliqué depuis Juin 2017.
Force est de constater que ce calcul pourtant simplissime n’a en effet été publié par personne en 2 ans et 2 mois depuis…
Il y a bien d’autres points qui n’ont pas été détaillé dans la TRM et qui peuvent être travaillés par quiconque aurait réalisé le module Gödel, certains pouvant déjà être travaillés par qui aurait réalisé le module Leibnitz déjà.
Les ajouts et améliorations de la TRM publiables (ayant un minimum d’auditoire se posant une question) ont tous été publiés sur creationmonetaire.info.
Il n’est pas utile de publier ce qui ne peut pas être compris.
Les cartons se remplissent, d’ici 160 ans tout aura été publié.
Certes, mais quand on fait découvrir la TRM à des nouveaux venus avec un background scientifique, on les renvoie… Vers la TRM. Et ensuite, si ils accrochent, ils peuvent aller approfondir sur creationmonetaire.info. En attendant, si ils trouvent des points critiquables, qui peuvent même être jugés de non-scientifique (le calcul de c sur un mode empirique typiquement, c’est le point central qui a été le plus critiqué), ils n’auront pas nécessairement envie d’aller approfondir sur creationmonetaire.info.
Je me demande une chose, la TRM étant sous licence GPLv3, est-il possible de faire évoluer sa version sans l’accord de l’auteur original ? Ou faut-il la forker ? Ou alors faut-il envoyer des propositions d’améliorations qui seront fusionnées par l’auteur dans la prochaine version ?
Franchement, ce calcul (qui est finalement très simple, c’est vrai) est vraiment génial. Bien plus solide que tout ceux qui ont été proposés jusqu’à présent pour déterminer c.
Faut envoyer des propositions d’améliorations, et au vu du résultat l’auteur la valide pour la branche principale pour une version 2.718.1 par exemple, oui.
Quelqu’un qui voudrait la modifier de son propre chef devrait lui donner un autre nom, et ce ne serait alors pas la branche historique.
J’ai déjà expliqué que la TRM était comme un logiciel.
Tu les renvoies vers la TRM ? Comme ça, sans avertissement ?
Tu te dis jamais : sur la partie Optimisation et espérance de vie, ça passera jamais, je vais passer pour un crétin ? T’es jamais tenté de les envoyer ailleurs, vers La TRM en détail, par exemple ?
Les scientifiques capables de dire :
Je soutiens la monnaie libre, y compris la valeur de 10%/an pour ‹ c ›, même si cette valeur est obtenue en utilisant un raisonnement fallacieux
je crois qu’ils ne sont pas beaucoup par rapport à ceux qui se disent :
Stop ! Ce raisonnement pour le calcul de ‹ c › est inacceptable, je n’ai pas plus de temps à consacrer à cette publication.
Ces derniers, s’ils t’entendaient parler de ces cartons qui se remplissent, ça les ferait bien rire. Pour les premiers, par contre, je pense que c’est plutôt un sentiment de consternation qui l’emporte.
Le raisonnement n’a absolument rien de fallacieux, c’est le même raisonnement qui est employé pour aboutir à cette formulation.
Qu’est-ce qui serait « inacceptable » ici ? Pourrais-tu rechercher par ailleurs comment se calcule un Décibel, et nous expliquer ici même en quoi il y eût une différence ?
Prétendre, affirmer, soutenir, croire, que des Lois physiques qu’elles qu’elles soient devraient être indépendantes de l’unité de mesure choisie pour les établir et en exprimer des mesures est véritablement idiot !
Ainsi celui qui croit que choisir l’unité de mesure 1 an = 1 révolution autour du soleil comme unité de temps, plutôt que de choisir une propriété locale de l’atome de Cesium, ou bien l’inverse de la Constante de Hubble n’aurait aucun impact sur les mesures dérivées de ces unités sur quelque élément physique que ce soit, celui là donc, ne comprendrait véritablement rien au sujet.
Ce ne seraient pas les premiers, et donc ?
Dans ce cas ils ne mériteraient pas l’appellation de « scientifiques ».
Au choix de l’inverse de la Constante de Hubble un ami scientifique n’a ni ri, ni manifesté de consternation, il m’a répondu immédiatement : « mais on manquerait alors de précision locale », ce à quoi je lui ai répondu « mais choisir une propriété locale n’implique-t-il pas de manquer de précision globale ? », ce à quoi seul un silence a répondu.
Bref, in-fine celui qui s’attarde sur la recherche de l’optimisation de la valeur de « c » dans la TRM, n’a véritablement pas l’esprit d’un scientifique.
Il est comme celui qui étudiant Ptolémée en rejetterait tout sous prétexte qu’avec Mercure ça ne marche pas. Ce qui serait véritablement idiot convenons en, car Ptolémée a bâti un ensemble descriptif absolument magnifique.
Et celui qui s’attacherait à une valeur de « c » telle que recherchée par la TRM, que ce soit dans sa première, deuxième, ou troisième formulation, comme quelque chose de sûr, qu’il ne faudrait absolument pas établir autrement, s’y attacher coûte que coûte, n’aurait véritablement pas les capacités de compréhension non plus.
Celui qui enfin s’attacherait coûte que coûte à la croyance qu’une monnaie libre est une solution, un chemin à suivre, une vérité qui mènerait à une économie libre serait tout autant dans l’erreur que celui qui s’attacherait à croire que c’en ne serait pas le chemin.
Ton calcul est mathématiquement correct, et il n’introduit pas de problèmes d’unités. Toutefois…
Le principe du calcul de « c » étant que la part de monnaie restante non-coproduite par les vivants, est de même ampleur que le cumul des décès de cette même génération.
… je ne suis pas sûr de bien comprendre ce principe. Pourquoi devrait-il y avoir un rapport, pour un membre, entre le nombre de décès par naissance durant sa vie avant un date donnée et la quantité de monnaie maximale qu’il lui reste à produire ? Pourquoi peut-on appliquer ce principe à différentes dates ? Suivant la date choisie t, le résultat de ce calcul de c peut varier énormément en décroissant avec t de l’infini à 0.
Ce n’est pas pour un membre, mais pour une génération de même âge.
Cette génération née en « t », de 1000 au départ n’est plus que 996 en t + 40 ans. Ce qui leur manque, non pas « à produire », mais pour atteindre la moyenne en t + 40 ans est considéré comme étant la part de ceux qui sont partis.
Ce qu’on pourrait aussi résumer par : la moyenne est atteinte pour les vivants, hors la part des morts.
Le calcul donnera en effet des taux tout à fait différents selon la date choisie pour atteindre la moyenne selon ce même principe.
Tout dépend du choix des humains quant au taux in-fine, bien entendu. C’est pourquoi ce point n’a in-fine aucune sorte d’importance cruciale.
S’attacher à ce point encore une fois n’est que la manifestation d’un voile quant à la nécessité de l’expérience, il n’y a ici aucun point indépassable.
Je ne vois aucun problème à voir apparaître des monnaies libres à c = 1% / an ou à c = 50% / an, je vois juste immédiatement la date d’atteinte de la moyenne ainsi que l’épargne disponibles, les deux jouant sur l’attrait que peut estimer l’un ou l’autre sur l’objet commun.
OK, mais je penche plutôt pour un autre principe. Cela m’est venu après ta conférence à Douarnenez.
Une grande valeur de c entraîne une dépréciation rapide, en DU, des sommes précédemment stockées, ce qui complique l’utilisation de la monnaie. Si on a le choix entre plusieurs valeurs possibles de c, il vaut donc mieux choisir la plus faible.
Les personnes meurent en moyenne à 80 ans, mais ce n’est qu’une moyenne, l’âge de décès étant dispersé autour ce cette moyenne. Si l’on veut que tous aient à peu près créé la même part de monnaie (en supposant qu’ils commencent à la naissance), il faudrait que pour un décalage d’un (ou plusieurs) écarts-types, la quantité de monnaie créée varie peu (en DU). Cela est favorisé par une valeur élevée de c.
Ces deux critères ayant des effets opposés sur la valeur de c, il reste à trouver un compromis. Ce n’est pas une solution, mais une piste de recherche.
Du moment que la compréhension relative à la durée de vie limitée est intégrée, ça me paraît tout à fait bien. Je t’encourage à mettre en équations ce principe et à voir comment il te permettrait de trouver une valeur pour c.
Tout à fait, j’aimerais tout de même souligner que ça a un impact sur la part relative de monnaie des premières générations par rapport à toutes les autres. En effet, si on réfléchi dans le référentiel moyenne :
Le premier DU est versé, M(0) = N(0)*DU(0). Ensuite, si le nombre de membres restent stable, le DU ne fait que diminuer, mais converge vers une limite.
Pourquoi ne pas commencer direct à la limite ? Et bien parce que sinon le premier DU représenterait une part relative de monnaie importante par rapport à la part relative du deuxième DU.
Finalement, les membres vieillissent, mais la monnaie aussi : au premier DU elle a 1 jour, au deuxième DU elle a 2 jours… le DU diminue, mais une fois que la monnaie a atteint l’age moyen de ses membres, elle n’a plus à diminuer.
Si la monnaie et les humains étaient immortels avec une population fixe, comme tu le dis, finalement, le « c » serait arbitraire, c’est à dire la part relative du DU par rapport à la moyenne. Il ne serait qu’un ratio de redistribution.
Mais la monnaie libre a un début, et par respect à la symétrie temporelle, il convient de diminuer la part relative des premiers DU par rapport à tous les suivants.
Je ne sais pas si c’est clair ![]()
J’avais commencé un calcul qui décomposait le DU dans le référentiel moyenne dont une part dépendait de l’âge de la monnaie. Ya plus qu’à !
Ce n’est pas vraiment le sujet du fil qui traite de principes permettant de calculer une valeur pour « c ».
Par contre ce que tu viens d’exprimer a un rapport avec la formule choisie pour le DU. Tu peux lire à ce sujet :
Justement, j’allais ouvrir une discussion intitulée Symétrie temporelle et fixation de c à 0,1 ! Car lorsque je présente la monnaie libre et la Ğ1, j’ai des difficultés à expliquer le choix du taux c par la symétrie temporelle.
Jusqu’à présent, je pouvais dire que c = ln (ev/2) / (ev/2) = 0,0922 arrondi à 0,1 et l’expliquer par « la masse monétaire doit être multipliée par 40 en 40 ans », mais sans pouvoir justifier cette contrainte. Comme atteindre la moyenne prendrait l’éternité avec le seul versement des DU, il s’agit uniquement de décider à quelle vitesse les vivants s’en rapprochent. Pour l’atteindre à 1/p près en T années, il faut que c = ln( p)/T. Avec la nouveauté faisant l’objet de cette discussion, c = ln(1/x)/A, x étant le taux de mortalité à l’âge A : on prend p=1/x et T=A en un point choisi sur la courbe des taux de mortalité. Très bien, mais je remarque qu’il n’y a plus de notion de symétrie temporelle. Comme l’a relevé @cuckooland, le choix du point, et donc de c, est maintenant qualifié d’empirique.
Remarque : dans d’autres domaines, on exprime la vitesse de rapprochement de l’asymptote au moyen de la demi-vie. Celle correspondant à c=0,1 est T = ln2/40 = ~7 ans. On pourrait aussi discuter et réfléchir sur la base de ce paramètre.
Cependant, la TRM (solutions) pose clairement qu’il s’agit d’équilibrer les intérêts des entrants et des sortants. Mais est-il opportun de distinguer les entrants (âgés de moins de 40 ans) et les sortants (de plus de 40 ans) dans un système où le total des DU reçus par une personne dépend déjà directement de la durée de son appartenance à la communauté ? Ma vision est que les bénéficiaires d’un c élevé ne sont pas les entrants, mais tous ceux qui détiennent moins que M/N, puisque cela fait croître leur solde plus vite. Les nouveaux venus en font partie car ils partent de zéro, mais ils n’y restent pas si leur activité économique leur rapporte suffisamment pour franchir la moyenne. À l’inverse, les bénéficiaires d’un c faible ne sont pas forcément les sortants, mais ceux qui détiennent plus que M/N, puisque cela fait décroître leur solde plus lentement.
Tout cela me conduit à penser que choisir c (et donc la force d’attraction de la moyenne), c’est en réalité choisir le taux de redistribution de la monnaie, de ceux qui ont plus vers ceux qui ont moins. C’est donc, malheureusement, une question purement politique. Cela m’ennuie beaucoup d’arriver à cette conclusion car j’aurais préféré que la beauté d’une symétrie choisisse pour nous.
Qu’est-ce qui ne serait donc « pas empirique » quand il existe un choix ? Par exemple peut-on dire qu’une monnaie établie avec c = 15% / an ou une monnaie avec 7% / an ne serait pas libre ? Qu’en dis-tu ?
Comment qualifierais-tu une monnaie avec c = 100% / an, et une monnaie avec c = 1% / an ? Comment justifies-tu cette qualification ?
Les DU sont produits, ou coproduits, mais ne sont « reçus » de nulle part, ils ne proviennent pas d’un compte tiers qui les distribuerait.
Ceux qui détiennent M/N ne sont-ils pas amenés à pouvoir détenir plus que M/N ? Dès lors comment seraient-ils à la fois bénéficiaires d’un c élevé, quand cela les défavorisera quand ils détiendront plus que M/N ? Sur quoi se base leur « bénéfice » ? Hier ? Maintenant ? Demain ? Sont-ils donc « bénéficiaires » tout le temps ? S’ils ne sont pas bénéficiaires « tout le temps » selon « toutes leurs situations », alors donc, que signifie « bénéfice » ? Si par ailleurs il se trouvait un bénéfice sûr à toujours détenir moins que la moyenne, que tout le monde alors vise cet objectif, comment cela serait-il donc possible, que tout le monde possède moins que la moyenne de tout le monde ?
Tu peux étudier le module Galilée (le mieux étant de le réaliser soi-même) où cette double nature est implacablement démontrée.
Où est le malheur quand il est démontré par la Ğ1, que ce choix a été fait par plus de 2100 humains en 2019 ? Faudrait-il à ton avis que ces humains n’eussent pas eu le choix d’adopter une monnaie libre ?
Quant à ceux qui ont choisi une monnaie comparable à un paramètre de c = 0, ils existent aussi, c’est le cas du bitcoin, où les nouveaux entrants n’ont plus de possibilité de créer une part de monnaie équivalente à celle des premiers entrants, et ce dès 10 ans après son lancement.
On voit donc que le choix politique qui permet de choisir c = 0, ou bien c = 10% / an existe bel et bien par ces deux expériences vérifiables.
Un choix arbitraire.
Bien sûr, le solde de toute personne peut traverser la moyenne de nombreuses fois au gré de son activité économique. Je parle du groupe qui est au-dessus/en dessous à un moment donné, comme on parle des entrants et des sortants.
Comme je l’ai dit, j’aurais préféré que la beauté d’une symétrie choisisse pour nous. Il reste vrai que la monnaie libre n’est pas une politique économique, mais les développeurs, y compris ceux qui forkeront, font un choix politique quand ils fixent c. Les 2100 membres de la toile ont choisi un système où c est déjà fixé. Ceci dit, je n’ai rien contre le taux de 10 %. Je suis juste incapable de le justifier par une symétrie temporelle. Cela n’entame pas mon enthousiasme pour le concept et l’expérience grandeur nature.
Que serait donc la propriété « bénéficiaire pour tous tout le temps », peux-tu décrire un tel état ?
Pourtant j’y arrive de mon côté plutôt facilement même :
Avec c = 10% la symétrie temporelle est assurée pour t = 40 ans, dans le sens où tout individu présent ou futur est assuré d’atteindre en coproduction relative la moyenne de la monnaie à 1/40ème près = 2,5 % près, soit 97,8% de la moyenne.
Pourrais-tu décrire à un auditoire à quel % la moyenne est approchée en t = 40 ans, pour c = 50% / an et pour c = 2% / an ?
Et de la même manière pourrais-tu décrire à un auditoire quels c correspondent à l’atteinte de la moyenne à 97,5% près en t = 20 ans ainsi qu’en t = 80 ans ?
Ensuite n’est-il pas possible de montrer la courbe des décès par âges et d’estimer sur quels points il est préférable de chercher une atteinte de la moyenne, et sur lesquels il est préférable de ne pas chercher ? Par exemple, est-il intéressant de chercher une atteinte de la moyenne pour t = 350 ans ? Pourquoi ?
Enfin es-tu en mesure de révéler selon ces différentes valeurs de « c » les stocks d’épargne moyens exprimés en DU annuels, et de les comparer entre eux ?
Prétends-tu que le choix c = 0,1% / an, ou c = 150% / an, ou c = 10% / an, est parfaitement arbitraire, et que tirer au sort entre ces valeurs vaut tout aussi bien que d’estimer une recherche de symétrie temporelle ?
La propriété « un DU par personne à intervalle régulier » bénéficie à tous, tout le temps et même partout. Symétrie spatiale.
Non, je répondais juste à ta question. Un choix qui n’est pas empirique peut par exemple être arbitraire. On s’égare, et je recentre : avant la publication du 5 août, la valeur de c était fixée d’une manière dictée (peut-être) par une symétrie, maintenant c est choisi de manière empirique. Ce qui est plutôt bien quand on n’a pas de méthode de calcul.
Ta justification de la symétrie temporelle :
Ok pour les 40 ans, qui sont ev/2. Mais la valeur 1/40 est un choix qui ne relève pas d’une symétrie. C’est juste l’inverse du même nombre, ce nombre ne représentant plus une durée.
Oui, ainsi que les autres questions sauf la dernière que je n’ai pas spécialement étudiée. Mais cela ne répond pas à cette question de symétrie.
Je m’absente pour plusieurs jours, ce qui me réduira au silence. ![]()
Quand j’ai plus que M/N, même si je bénéficie du DU au sens où je l’ai en plus, en prenant en compte la globalité de l’économie il me défavorise (que ce soit en M, M/N, DU ou Ğ1)…
Si la propriété « bénéficiaire » est définie par « bénéficie », tu comprendras que tu tombes dans une récursivité infinie, qui ne définit rien. Donc pour résoudre ton questionnement, tu dois d’abord commencer par définir précisément les termes de la question.
Non, c n’a jamais été choisi de manière empirique ! Tu confonds deux choses : la définition du calcul de c qui n’a rien d’empirique, et qui répond à une recherche de symétrie temporelle bien définie d’une part, et la valeur de c d’autre part qui, elle, ne peut être qu’empirique !
Je cite : « l’approche qui se fonde sur les données empiriques de l’espérance de vie mais aussi de son corollaire : le taux de mortalité ».
Toute valeur dimensionnée est empirique, ainsi la valeur de la vitesse de la lumière (en m/s) est empirique, la valeur de la constante de gravitation terrestre (en m/s²) est empirique, tout comme la valeur de la constante de Planck, ou celle de la constante de Hubble etc…
PI = 3,14159… lui n’est pas une valeur empirique, c’est un nombre sans dimension, que l’on peut retrouver par le calcul sans réaliser aucune mesure dans le monde physique phénoménal.
Tu dois donc éclaircir et préciser ta compréhension du sujet en ne mélangeant pas les propriétés.
Mais la mesure de la vitesse de la lumière, qui possède une propriété de symétrie, qui est son invariance par changement de référentiel, ne repose absolument pas non plus sur une symétrie ! Et on ne la connaît qu’à un % près, qui ne pourra jamais atteindre une quelconque précision absolue. Ce qui est vrai de toute valeur empirique comme la constante de planck, de Hubble, de gravitation etc.
Tu confonds donc la précision recherchée, qui répond à une double contrainte (ni trop faible, ni trop haute), avec la propriété de symétrie.
Toute valeur de c > 0 pour une monnaie libre répond à la propriété de symétrie temporelle, mais pas avec le même degré de précision.
La symétrie spatio-temporelle est définie par :
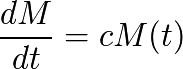
Qui ne dépend pas de la valeur de c.
De la même façon qu’on s’accomode très bien d’une valeur de C = 300 000 km/s, sans toucher à ses propriétés de symétrie, mais pour aller loin dans la précision sur certaines applications le degré de précision ne suffit pas.
De la même façon c = 100% / an, répond parfaitement bien à la propriété de symétrie temporelle, mais manque de précision relativement à la recherche d’une valeur relative du DU suffisamment haute pour répondre à des besoins plus importants.
Par exemple il a déjà été modélisé une monnaie libre pour une école de commerce, dont la durée de passage pour les étudiants est de 3 ans, dans ce cas c a été optimisée pour v = 36 mois par le calcul théorique : c = ln(v/2)/(v/2), donnant un résultat empirique de c = ln(18) / 18 = 16% / mois, et la vérification graphique a permis de confirmer ce choix pour c comme étant jugé optimal pour ce cas particulier. Des valeurs proches faisant aussi parfaitement l’affaire.
Quand on fait les plans d’une maison, on ne compte pas ni en angströms, ni en Parsecs.
On peut se demander pourquoi, bien que le mètre soit théoriquement suffisant, on s’invente ainsi des unités de mesures qui en diffèrent. Laurent Nottale a développé la théorie d’échelle pour tenter de comprendre certaines propriétés dues à ces changements d’échelle justement.
Tu dois donc redéfinir tes termes, clarifier tes questionnements, distinguer le théorique de l’empirique, voir où la symétrie existe ou pas, ainsi qu’étudier ce que signifie exactement une recherche de précision et dans quel domaine d’application.