Bonjour,
Je lis sur ce fil des gens qui discutent en prenant cette hypothèse comme point de départ :
Le dividende universel devrait augmenter entre 5 et 10% par an
Pour ceux qui ont bien compris la TRM, ceci est tout bonnement faux. Donc le prendre comme point de départ d’un raisonnement ne peut aboutir qu’à des résultats tout aussi faux.
edit - NB : je ne prétends pas que cette assertion est toujours fausse. Je dis simplement qu’elle n’est pas nécessairement vraie et donc ne peut pas être utilisée comme point de départ d’un raisonnement.
Je me suis dit que c’était l’occasion de faire un peu de pédagogie. La TRM prend comme postulat de base que chaque individu, à uné époque, doit créer la même part de monnaie que ses contemporains, et que la masse monétaire doit croître de façon constante. C’est ce qu’on appelle la symétrie spatio-temporelle.
NB - Si vous n’êtes pas d’accord avec mes propos, prenez le temps de poser les calculs et de tourner sept fois vos mains sur votre clavier avant de répondre. Si vous voulez approfondir, l’auteur de la TRM a prévu des exercices, dont voici le premier : module Gallilée.
Rappels de la TRM
Symétrie spatiale
La symétrie spatiale, c’est le fait que, pour une même plage de dates (donc à la même époque), deux individus créent le même montant.
Soit, dans la notation utilisée par la TRM :
dM / dx = 0
si on veut le noter de façon plus compréhensible, étant donné deux individus (a) et (b) et M la monnaie que chacun crée :
M(a) = M(b)
Donc M(a) - M(b) = 0
Si on prend ‹ x › comme voulant dire ‹ tout individu › M(a) - M(b) = 0 se traduit ‹ La variation de M entre chaque individu x est nulle ›, soit :
dM / dx = 0
Symétrie temporelle
La symétrie temporelle, c’est le fait que les générations successives créent une même portion de monnaie. Autrement dit c’est le fait que, quelle que soit les époques, la masse monétaire totale croisse de façon constante.
La formule donnée par la TRM est celle-ci :
M(t+1) = (1+c) x M(t)
Où on trouve le fameux paramètre c. On peut aussi l’écrire :
M(t+1) = M(t) + (c x M(t))
Ou, écrit en bon français :
Pour respecter la symétrie entre génération relativement à la masse monétaire, la masse monétaire doit augnenter d’un facteur (c) pour un même intervalle de temps (t)
. On observe que c’est la masse monétaire totale, et non le dividende universel, qui croît de façon constante. On observe également que l’expression de la croissance de la masse monétaire ne fait jamais intervenir ni la population (N), ni le dividence universel.
Calcul du DU
En partant de ces prémisses (je vous laisse aller voir la démonstration), la TRM aboutit à un résultat valable pour N constant :
N étant le nombre d’individus dans la zone monétaire étudiée.
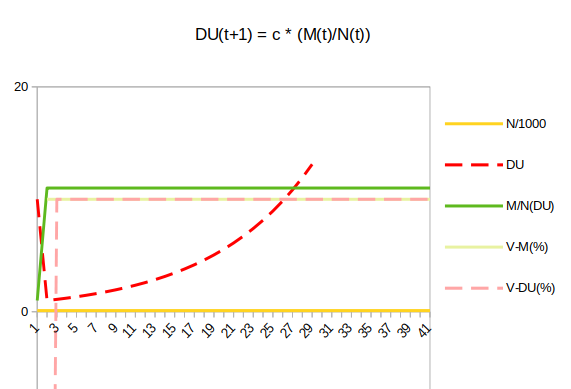
DU = c x (M/N)
ce qui est équivalent à
DU = (c x M) / N
Optimisation et espérance de vie
Plus loin, la TRM propose une valeur de c adaptée à l’espérance de vie humaine, et aboutit à un résultat compris entre 5 et 10% par an.
un autre calcul qui prend en compte le taux de mortalité aboutit à une valeur comprise entre 2,2% et 14,33% par an.
Application chiffrée : simulation sur deux ans
Pour les exemples chiffrés qui suivent, on prend :
-
c = 10%.
-
M(t) = 1000
-
N(t) = 10
-
t+1 = t + 1 an
N stable entre t et t+1
à l’instant t :
M/N = 1000 / 10 = 100
Donc à T+1
DU = c(M/N) = 0.1 * (1000 / 10) = 0.1 * 100 = 10
Et donc :
M(t+1) = M(t) + N * DU = 1000 + 10 * 10 = 1100
On a bien M(t+1) = (1+c) x M
N en croissance entre t+1 et t+2 (application naïve de DU = c x M/N)
On considère qu’à T+2, N a fortement augmenté et que la population est passée de 10 à 100 en un an. On a donc :
DU = c(M/N) = 0.1 * (1100 / 100) = 0.11 * 10 = 1.1
Le DU est donc de 1.1 : dix fois moins que si la population était stable ! Il n’a pas augmenté de 10%, loin de là, il a baissé de 89% !
Pour autant :
M(t+2) = M(t+1) + N * DU = 1100 + 100 * 1.1 = 1110
On a toujours M(t+1) = (1+c) x M
N en croissance entre t+1 et t+2
En première analyse, il semble injuste que les 90 personnes arrivées à t+2 créent moins de monnaie sur un même intervalle, que les 10 présents à t0. La TRM prévoit ce souci et propose plusieurs solutions, dont la plus facile à comprendre est cette formule :
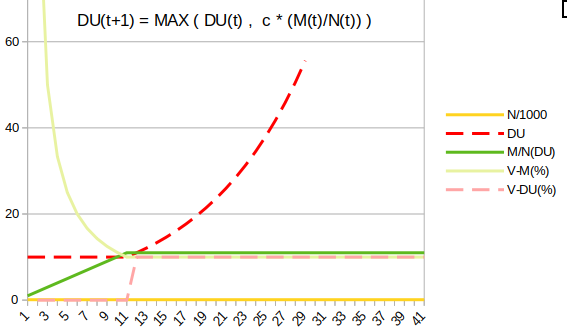
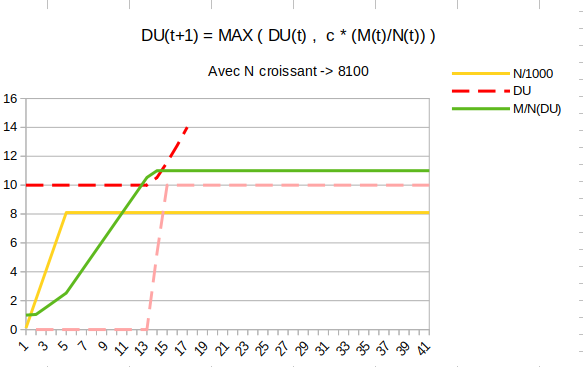
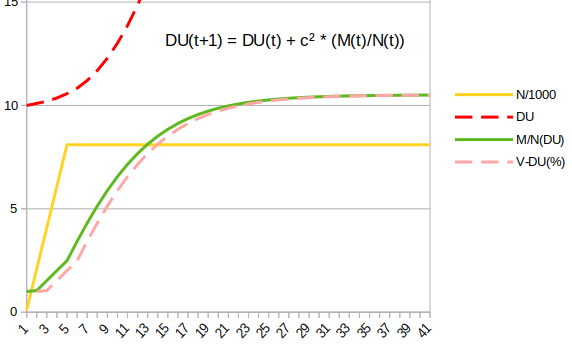
DU(t+1) = MAX[ DU(t) , c(M(t)/N(t)) ]
En appliquant cerre formule, le DU(t+2) serait resté constant par rapport au DU(t+1), il n’aurait donc pas augmenté de 10%.
Et on aurait :
M(t+2) = M(t+1) + N * DU(t+1) = 1100 + 10 * 100 = 2100
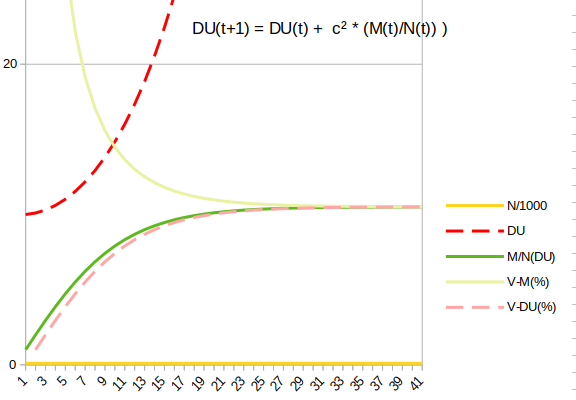
… On voit donc que si on applique une formule pour éviter la baisse de valeur du DU et que N est croissant, alors M augmente très fortement, bien plus que c x M Pour contrebalancer cela, le DU reste stable après une phase de croissance forte jusqu’à ce que c(M/N) dépasse le DU en vigueur avant cette phase de croissance. (vous pouvez faire les calculs, qui sont assez simples)
On peut en conclure que Si N est en croissance, alors DU(t+1) sera toujours inférieur à (1+c) x DU(t)
Voir aussi, pour comprendre la formule utilisée dans Duniter, le post Dividende universel d’ordre N.
Conclusion concernant un DU à +10% par an
Il y a donc deux façons d’avoir un DU dont la valeur augmente de 10% par an :
-
ne plus avoir de nouveaux entrants (je doute fort que les membres de ce forum et les membres de Ğ1 le souhaitent)
-
en maintenant la croissance de N actuelle, dépasser, et de loin, le taux de croissance monétaire
cfixé à 10%. On se place alors hors des valeurs decproposées par la TRM. Et dans ce cas, il faut prévoir une phase de « rattrapage », comme le fait la formuleDU(t+1) = MAX[DU(t), (c(M(t)/N(t)). Je préfère, et de loin, avoir un DU qui croît peu mais régulièrement, qu’un DU dont la valeur croît irrégulièrement voire stagne en fonction de la croissance de la population. Comment réagiraient les futures membres en voyant qu’ils ont un DU qui stagne alors que leurs prédécessaurs avaient un DU croissant ? mal, sans nul doute.